(suma zawartości komórek C2 i D2),
nieprawidłową byłaby formuła =10+5 (suma liczb 10 i 5)
Podstawowym przeznaczeniem arkuszy kalkulacyjnych jest wykonywanie wszelkich obliczeń, najczęściej na dużej ilości danych. Obliczenia sprowadzają się do wykonywania działań matematycznych oraz wykorzystania różnorodnych funkcji - statystycznych, matematycznych, logicznych, księgowych, finansowych i innych. Ponieważ obliczenia bardzo często mają charakter powtarzających się operacji rachunkowych na dużych ilościach różnych danych, działania i funkcje zapisuje się w formułach.
Formuła jest to rodzaj wzoru według którego wykonuje się obliczenia.
Stosowanie formuł ma sens tylko wtedy, gdy w ten sam sposób wykonuje się wiele obliczeń. Na przykład - formułę zdefiniowaną dla obliczenia wartości jednego towaru wykorzystuje się dla obliczenia wartości innych towarów (wartość każdego towaru oblicza się w taki sam sposób - mnożąc ilość razy cenę jednostkową).
W formułach stosuje się operatory arytmetyczne i operatory porównań:
+ dodawanie, - odejmowanie, * mnożenie, / dzielenie, ^ potęgowanie,
= równy, < mniejszy , > większy , <= mniejszy lub równy, >= większy lub równy, <> nie równy.
Formułę wprowadza się do komórki wpisując ją na pasku formuły
(można również w komórce po jej dwukrotnym kliknięciu)
zawsze zaczynając znakiem = (ewentualnie znakiem +).
W formule należy się odwoływać do zawartości komórek podając ich adresy,
a nie do wartości wprowadzonych w komórki. Wówczas, w przypadku zmiany wartości w komórce, aktualizowana będzie wartość formuły.

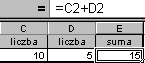
| W przykładzie poprawną formułą jest =C2+D2 (suma zawartości komórek C2 i D2), nieprawidłową byłaby formuła =10+5 (suma liczb 10 i 5) |
Po uaktywnieniu komórki zawierającej formułę na pasku formuły wyświetlana jest formuła, zaś w komórce wartość tej formuły.
Poniższa tabela przedstawia kilka przykładowych formuł.
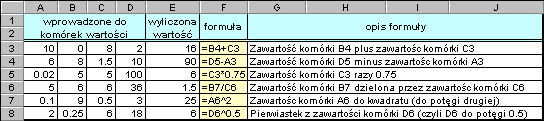
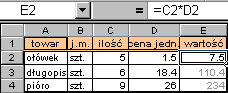
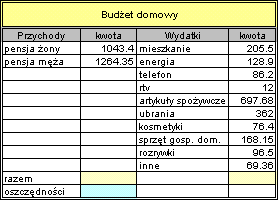
| Do komórki E2 wprowadzamy formułę =C2*D2 według której obliczana jest wartość ołówków (iloczyn zawartości komórki C2 - ilość i zawartości komórki D2 - cena jedn.). Ponieważ wartość długopisów, piór i wszystkich innych towarów oblicza się w analogiczny sposób, raz napisaną formułę w komórce E2 kopiujemy do odpowiednich komórek w których mają być wyliczone wartości towarów. |
Jedną z częściej wykonywanych w arkuszach obliczeniowych operacji rachunkowych jest sumowanie wartości w sąsiadujących komórkach w kolumnach i wierszach. Wykorzystuje się w tym celu polecenie Autosumowanie.
Poniższy przykład przedstawia wykorzystanie Autosumowania do wyliczenia łącznej wartości towarów.
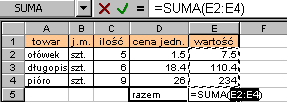
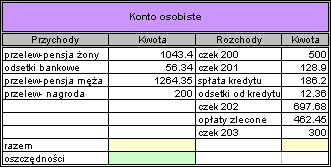
| Formuła w komórce E5 zawiera funkcję suma (więcej wiadomości o funkcjach arkusza zawiera następny podrozdział) wstawioną za pomocą przycisku   znajdującego się na standardowym pasku narzędzi. znajdującego się na standardowym pasku narzędzi. |



W arkuszach kalkulacyjnych wykorzystywane są różne rodzaje odwołań, czyli adresowania. Umożliwiają one przede wszystkim korzystanie z danych umieszczonych w różnych częściach arkusza roboczego w jednej formule lub używanie wartości z jednej komórki w wielu formułach. Możliwe jest także odwoływanie się do komórek w innych arkuszach tego samego skoroszytu, do innych skoroszytów (odwołania zewnętrzne) i do danych w innych programach (odwołania zdalne).
Rozróżnia się trzy podstawowe rodzaje odwołań:
odwołania względne, odwołania bezwzględne i odwołania mieszane.
Istota wymienionych rodzajów odwołań widoczna jest najlepiej w trakcie kopiowania formuł zawierających te odwołania.
Przeanalizujmy przykład ilustrujący istotę wymienionych rodzajów odwołań.
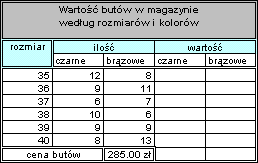
W sklepie sprzedawane są koszulki sportowe. Wszystkie mają tą samą cenę, natomiast różnią się rozmiarem i kolorem. Zadanie polega na obliczeniu wartości koszulek według rozmiarów i kolorów.
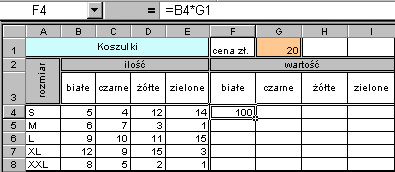
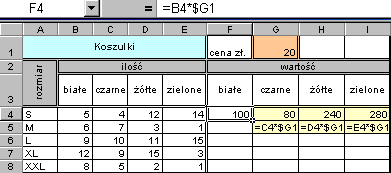
| W komórce F4 obliczamy wartość koszulek białych rozmiar S. Formuła wygląda jak na rysunku obok. Była by formułą poprawną gdyby chodziło o obliczenie tylko wartość tych koszulek. |
Możemy spróbować wykorzystać formułę = B4*G1 do obliczenia wartości wszystkich koszulek białych (kopiując w dół) lub
wszystkich koszulek rozmiar S (kopiując w prawo).
Efekty takich prób widać na rysunkach poniżej.


Nie są to efekty zadawalające. Przyczyną tego jest wykorzystanie w formule = B4*G1 odwołań względnych do komórki G1 (zawierającej cenę).
Odwołanie względne to takie odwołanie, którego adres przy kopiowaniu ulega zmianie o odpowiednią liczbę wierszy i liczbę kolumn w stosunku do położenia źródłowego w zależności od kierunku kopiowania.
W przykładzie powyżej kopiowanie formuły = B4*G1 w dół powodowało kopiowanie "przepisu"policz iloczyn komórek położonych o jedną niżej niż ta w której jesteś,
zaś kopiowanie w prawo policz iloczyn komórek położonych o jedną w prawo niż ta w której jesteś.
Stąd uzyskanie niezadowalającego efektu.
Wracając do przykładu.
Aby udało się obliczyć wartości wszystkich koszulek białych formułę = B4*G1 trzeba poprawić w ten sposób, że do komórki G1 należy odwoływać się w sposób mieszany.
W tym celu w odwołaniu umieszcza się przed cyfrą 1 oznaczającą numer wiersza symbol $ (zakotwiczenie w wierszu 1).
Poprawiona formuła będzie miała postać = B4*G$1.
Natomiast obliczając wartości koszulek rozmiar S należy poprawić formułę umieszczając$ przed literą G oznaczającą kolumnę w adresie(zakotwiczenie w kolumnie G).
Poprawiona formuła będzie miała postać = B4*$G1.
Efekty poprawek w formułach widoczne są na rysunkach poniżej.
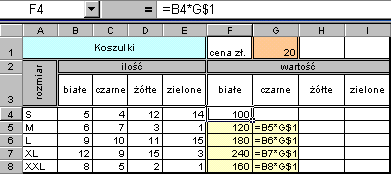
Odwołanie mieszane, to takie odwołanie, w którym przy kopiowaniu adres kolumny ulega zmianie, a nie ulega zmianie adres wiersza, lub ulega zmianie adres wiersza, a nie ulega zmianie adres kolumny w stosunku do położenia źródłowego.
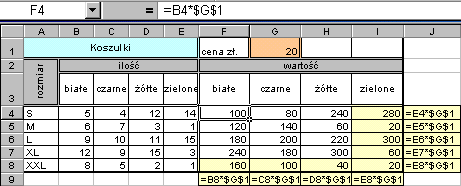
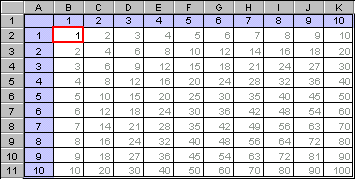
w przykładowym zadaniu należy obliczyć wartości koszulek we wszystkich rozmiarach i wszystkich kolorach. Aby udało się to zrobić wpisując jedną formułę, a następnie kopiując ją, powinna ona zawierać odwołanie bezwzględne do komórki G1 zawierającej cenę. Taka formuła ma postać = B4*$G$1. Wpisanie takiej właśnie formuły i skopiowanie jej do pozostałych komórek jest prawidłowym rozwiązaniem przykładowego zadania.
Zastosowanie formuły zawierającej odwołanie bezwzględne w rozwiązaniu przykładowego zadania ilustruje poniższy rysunek.




W arkuszach kalkulacyjnych są dostępne wszystkie działania matematyczne, ale umiejętność ich wykorzystania w formułach w bardzo wielu przypadkach okazuje się nie wystarczająca. Nawet w dość prostych arkuszach obliczeniowych wykorzystuje się funkcje.
Funkcja jest wstępnie zdefiniowaną formułą wykonującą obliczenia na wartościach zwanych argumentami. w programie jest dostępnych kilkaset funkcji (nie wszystkie przy standardowej instalacji).
Wprowadzając formuły zawierające funkcje najczęściej korzysta się z przycisku

 na standardowym pasku narzędzi, lub z polecenia Wstaw/Funkcja...
na standardowym pasku narzędzi, lub z polecenia Wstaw/Funkcja...
(można też z klawiatury wpisać na pasku formuły).
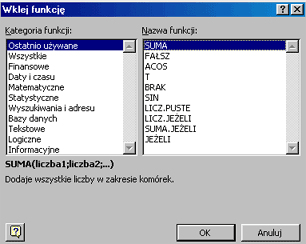
| W obydwu przypadkach otwiera się okno widoczne na rysunku obok (czasami
zwane kreatorem funkcji - od nazwy we wcześniejszych wersjach programu). W lewym panelu okna wyświetlane są kategorie funkcji, w prawym nazwy funkcji w wybranych kategoriach. W dolnej części okna wyświetlana jest składnia zaznaczonej funkcji i opis funkcji. |
Po wybraniu żądanej funkcji pojawia się okno - paleta formuł. Okna palety różnią się zawartością, bowiem ich zawartość zależy od składni funkcji.
Poniższe okno przedstawia paletę formuły funkcji suma oraz pasek formuły z wypisaną na nim formułą zawierającą tą funkcję.
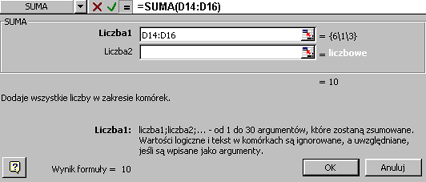
| Paleta formuł wyświetla zawsze nazwę funkcji, wszystkich jej argumentów, opis funkcji i argumentów, bieżący wynik funkcji i wynik całej formuły. |
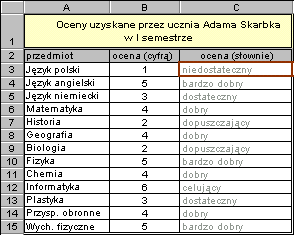
Składnia niektórych funkcji jest bardzo prosta. Dotyczy to takich funkcji jak suma, iloczyn, średnia, min, max, pierwiastek itp. Wstawiając taką funkcję do formuły rola użytkownika sprowadza się tylko wskazania argumentów funkcji. Poniższy przykład ilustruje wykorzystanie w formule funkcji ŚREDNIA dla obliczenia średniej ocen.

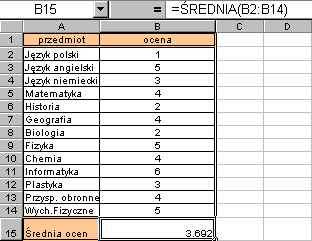
Formuła w komórce B15 zawiera funkcję ŚREDNIA dla argumentów z zakresu B2:B14.
Formuła =ŚREDNIA(B2:B14) wypisywana jest na pasku formuły, a wartość funkcji dla argumentów z zakresu B2:B14 wypisana jest w komórce.
Większość funkcji ma jednak nieco bardziej złożoną składnię. Wykorzystując je w formułach również należy określić ich argumenty, których najczęściej jest więcej i mogą mieć postać warunków, kryteriów itp.
Każda funkcja jest opisywana na palecie formuły. Zawsze w lewym dolnym rogu palety znajduje się przycisk  , który uruchamia pomoc na temat wybranej funkcji.
Pomoc zawiera opis funkcji, omówienie składni, wyjaśnienie pojęć występujących w składni oraz przykłady.
, który uruchamia pomoc na temat wybranej funkcji.
Pomoc zawiera opis funkcji, omówienie składni, wyjaśnienie pojęć występujących w składni oraz przykłady.

| Rysunek przedstawia otwarte okno pomocy funkcji matematycznej SILNIA. |
Poniższy przykład ilustruje wykorzystanie w formułach funkcji JEŻELI
(jej odpowiednikiem w StarCalc jest funkcja GDY).
Firma sprzedaje kilka produkowanych wyrobów. Znane są poniesione koszty i przychody ze sprzedaży. Wykorzystując funkcję JEŻELI należy określić tzw. wynik finansowy
(zysk - przychody wyższe od koszów, strata - koszty wyższe od przychodów).
Funkcja JEŻELI jest funkcją warunkową, wykorzystujemy ją w następujący sposób.
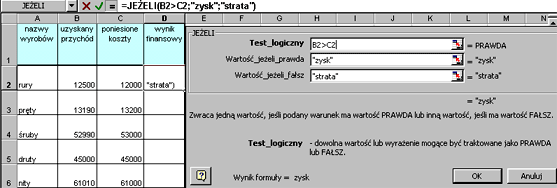
Określamy warunek, który ma być sprawdzany (Test_logiczny), w naszym przykładzie - czy przychody są wyższe niż koszty (B2>C2).
Następnie określamy "co się ma stać"
jeżeli warunek jest spełniony (PRAWDA) (napisać "zysk")
i "co się ma stać" jeżeli warunek nie jest spełniony (FAŁSZ) (napisać "strata").
Po wprowadzeniu do komórki D2 formuły =JEŻELI(B2>C2;"zysk";"strata") i skopiowaniu jej uzyskujemy następujący efekt.
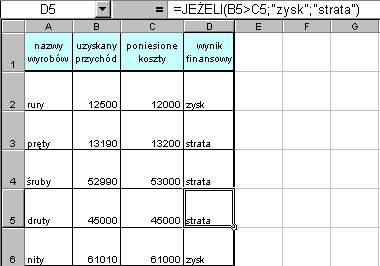
| Efekt, jak widać jest nie do końca zadawalający, ponieważ w komórce D5 wypisany jest tekst "strata", podczas kiedy koszty są równe przychodom. |
W naszym przykładowym zadaniu zastosowanie formuły =JEŻELI(B2>C2;"zysk";"strata") okazało się nie wystarczające, ponieważ formuła nie "rozpatruje" przypadku kiedy koszty są równe przychodowi.
Formuła, która w pełni zrealizuje zadanie powinna zawierać funkcję w funkcji.
Innymi słowy - argumentem jednej funkcji musi być inna funkcja. Takie funkcje nazywają się funkcjami zagnieżdżonymi.
Zatem poprawmy formułę zagnieżdżając funkcje w następujący sposób.
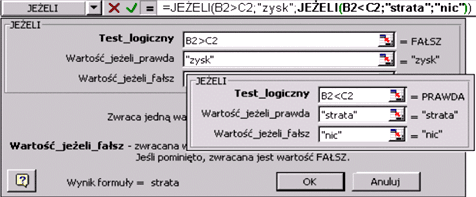
W analizowanym przykładzie formuła
=JEŻELI(B2>C2;"zysk";JEŻELI(B2<C2;"strata";"nic"))
realizuje zadanie następująco:
Jeżeli warunek B2>C2 jest spełniony pisz "zysk", w przeciwnym przypadku
sprawdź warunek B2<C2;
jeżeli jest spełniony - pisz "strata",
jeżeli nie jest spełniony - pisz "nic".
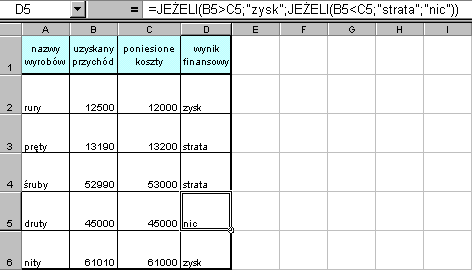
| Uzyskany ostateczny efekt przedstawia rysunek. |
Oto jeszcze jeden przykład wykorzystania zagnieżdżonych funkcji w formule.
Sprawdzić czy przykładowe dowolne liczby należą do przedziału (0;10).
Ponieważ przedział liczbowy jest przedziałem otwartym musi być spełniony warunek 0<liczby>10: co oznacza, że każda z przykładowych liczb musi być jednocześnie
większa od 0 i mniejsza od 10.
Zadanie zrealizuje następująca formuła =JEŻELI(ORAZ(B1>0;B1<10);"tak";"nie").
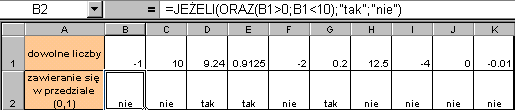
Powyższe zadanie jest przykładem wykorzystania w formule zagnieżdżonej funkcji ORAZ w funkcji JEŻELI.
W podobny sposób wykorzystuje się zagnieżdżone funkcje arkusza w formułach. Należy jednak pamiętać o tym, że formuła może zawierać nie więcej niż siedem poziomów zagnieżdżenia funkcji.
Poniższe zestawienie zawiera składnię i w miarę prosty (na ile to jest możliwe) opis najczęściej wykorzystywanych funkcji (nazewnictwo na przykładzie MS Excel 97).
| COS(kąt) | podaje wartość cosinusa podanego w radianach kąta - analogicznie SIN. |
| ILE.LICZB(wartość_1;wartość_2) | podaje ile liczb wystąpiło na liście podanych argumentów. |
| ILE.NIEPUSTYCH(wartość_1;wartość_2) | podaje ile niepustych wartości wystąpiło na liście podanych argumentów. |
| ILOCZYN(liczba_1;liczba_2) | mnoży wszystkie liczby i podaje w wyniku ich iloczyn. |
| JEŻELI(test_logiczny; wartość_jeżeli_prawda; wartość_jeżeli_fałsz) | podaje wartość_jeżeli_prawda jeśli podany warunek ma wartość PRAWDA, podaje wartość_jeżeli_fałsz jeśli podany warunek ma wartość FAŁSZ. |
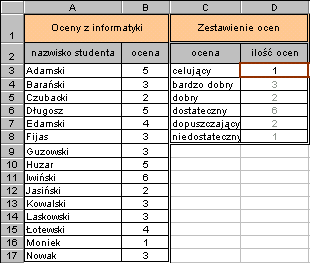
| LICZ.JEŻELI(zakres;kryteria) | zlicza liczbę tych komórek z podanego zakresu, które spełniają podane kryteria. |
| LICZ.PUSTE(zakres) | zlicza puste komórki w podanym zakresie. |
| LUB (wartość_logiczna_1; wartość_logiczna_2) | podaje wartość logiczną PRAWDA, jeżeli choć jeden warunek jest spełniony, w przeciwnym wypadku podaje wartość FAŁSZ. |
| MAX(liczba_1;liczba_2) | podaje największą wartość z podanych argumentów. |
| MIN(liczba_1;liczba_2) | podaje najmniejszą wartość z podanych argumentów. |
| MODUŁ.LICZBY(liczba) | podaje wartość bezwzględną liczby. |
| ORAZ (wartość_logiczna_1; wartość_logiczna_2) | podaje wartość logiczną PRAWDA, jeżeli wszystkie warunki są spełniony, w przeciwnym wypadku podaje wartość FAŁSZ. |
| PI() | podaje wartość stałej matematycznej . |
| POTĘGA(liczba;potęga) | podaje wartość podanej liczby podniesionej do żądanej potęgi. |
| RADIANY(kąt) | zamienia miarę stopniową podanego kąta na radiany. |
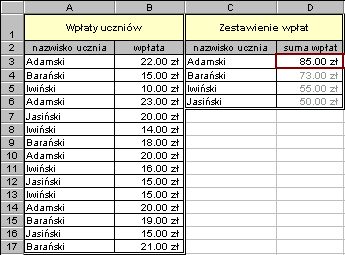
| SUMA.JEŻELI(zakres;kryteria;suma_zakres) | sumuje te komórki z zakresu sumowania, dla których odpowiednie komórki z podanego zakresu spełniają podane kryteria. |
| STOPNIE(kąt) | przekształca podany kąt wyrażony w radianach na stopnie. |
| ŚREDNA(liczba_1;liczba_2) | oblicza średnią arytmetyczną podanych argumentów. |
| ZAOKR(liczba;liczba_cyfr) | zaokrągla podaną liczbę do określonej liczby cyfr. |
W pracy z arkuszem kalkulacyjnym bardzo istotna jest umiejętność ochrony zawartości arkusza. Dzięki ochronie (zabezpieczeniu, protekcji) zapobiega się dokonywaniu zmian w całym skoroszycie, w określonym arkuszu lub w wybranym obszarze arkusza.
Każda komórka ma indywidualne możliwości ustawiania atrybutu ochrony (domyślnie ustawiona jest ochrona), który zaczyna działać dopiero po włączeniu ochrony całego arkusza. Zatem jeżeli ochrona dotyczy całego arkusza wszystkie komórki w arkuszu są zabezpieczone przed modyfikacją.
Jeżeli ochrona ma dotyczyć nie wszystkich komórek arkusza (w praktyce ochrona najczęściej dotyczy wszystkich oprócz wybranych komórek), to dokonuje się jej dwuetapowo.
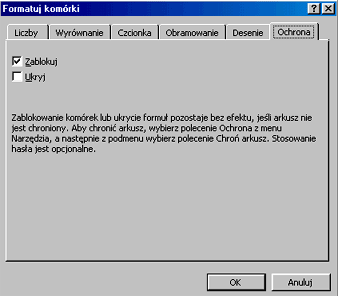
| Najpierw wybiera się komórki, które nie będą chronione oraz w Format/Komórki/Ochrona wyłącza pole wyboru Zablokuj. |
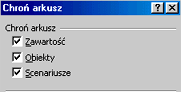
| Następnie wybiera się z menu Narzędzia/Ochrona/Chroń arkusz... w oknie dialogowym istnieje możliwość wyboru elementów podlegających ochronie i opcjonalnie - hasła. |
W przypadku próby modyfikacji chronionych komórek, arkusza czy skoroszytu pojawia się komunikat o ochronie.
Ćwiczenie 13.

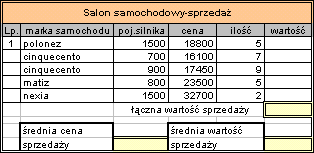
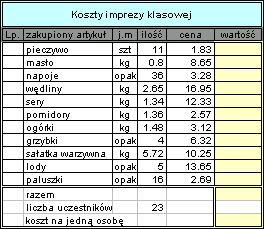
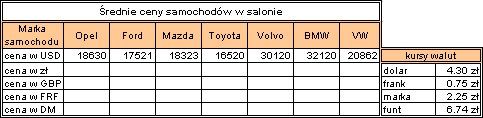
3. Uzupełnij poniższą tabelkę.
4. Oblicz: łączną wartość sprzedaży, średnią wartość sprzedaży, średnią cenę sprzedanego samochodu.
5. Dopisz pozycję: Polonez 1600, 5 szt. cena 21 700zł.
6. Spowoduj wyświetlanie cen i wartości w formacie waluty.
7. Oblicz średnią wartość sprzedaży i średnią cenę sprzedaży w zaokrągleniu do 1 zł.